El campo de la inteligencia artificial ha sido transformado por el desarrollo de las redes neuronales, un tipo de algoritmo de aprendizaje automático que se distingue por su profunda inspiración en la estructura y el funcionamiento del cerebro humano. Estas arquitecturas computacionales tienen como propósito fundamental capacitar a las computadoras para procesar datos de una manera que emule las complejas capacidades cognitivas humanas. Frecuentemente denominadas redes neuronales artificiales (ANNs) o redes neuronales simuladas (SNNs) , se componen de unidades interconectadas, conocidas como neuronas artificiales, que modelan de forma abstracta las neuronas biológicas.
La analogía con el cerebro biológico trasciende una mera etiqueta descriptiva; encapsula una ambición central de la inteligencia artificial: replicar la capacidad de aprendizaje y el procesamiento de información compleja que caracteriza al cerebro. Esta inspiración biológica no solo establece una expectativa sobre la flexibilidad, adaptabilidad y capacidad de generalización de estas redes, sino que también las diferencia sustancialmente de los algoritmos informáticos tradicionales. Mientras que los algoritmos convencionales operan bajo reglas explícitas y predefinidas, las redes neuronales, al igual que el cerebro, aprenden directamente de los datos. Esta aproximación basada en el aprendizaje marca un cambio fundamental en la forma de abordar problemas complejos, lo que explica su notable potencia en dominios como el reconocimiento de imágenes y el procesamiento del lenguaje natural.
Las redes neuronales se han consolidado como una herramienta computacional excepcionalmente potente, destacando en la resolución de problemas intrínsecamente difíciles para los algoritmos informáticos tradicionales. Ejemplos prominentes de estas aplicaciones incluyen el reconocimiento de imágenes y el procesamiento de lenguaje natural. La capacidad de estas redes para clasificar y agrupar grandes volúmenes de datos a una velocidad considerable constituye una de sus ventajas más significativas, convirtiéndolas en herramientas invaluables en la ciencia de la computación y la inteligencia artificial. La habilidad inherente de las redes neuronales para abordar problemas que resultan «difíciles de manejar» para los algoritmos convencionales, como la visión por computadora y el procesamiento del lenguaje natural, no solo valida su eficacia, sino que también señala un cambio de paradigma en el ámbito de la computación. Esto implica que las redes neuronales no son simplemente una mejora incremental de tecnologías existentes, sino una fuerza disruptiva que habilita la creación de aplicaciones previamente inalcanzables, marcando un antes y un después en el desarrollo tecnológico. Antes de su advenimiento, muchas de estas tareas eran inviables o extremadamente ineficientes, lo que subraya el impacto transformador de las redes neuronales en la capacidad de la tecnología para interactuar y comprender el mundo.
Un ejemplo tangible de la aplicación de redes neuronales en el mundo real es el algoritmo de búsqueda de Google. En el ámbito de la eficiencia operativa, tareas como el reconocimiento de voz o el reconocimiento de imágenes, que históricamente requerían horas de identificación manual por parte de expertos humanos, pueden ahora completarse en cuestión de minutos gracias a la velocidad y precisión inherentes a las redes neuronales.
1. Anatomía de una red neuronal artificial
Para comprender el funcionamiento de una red neuronal, es esencial desglosar su estructura interna y los componentes fundamentales que interactúan para procesar la información.
1.1. Capas: entrada, ocultas y salida
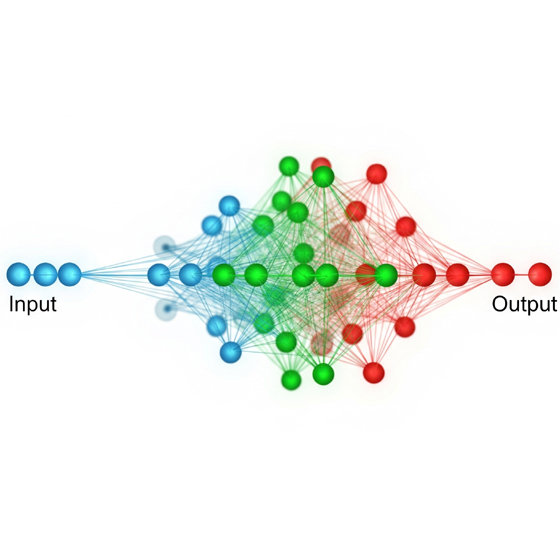
Una red neuronal típica se organiza en al menos tres tipos de capas distintas: una capa de entrada, una o varias capas ocultas, y una capa de salida. La capa de entrada está compuesta por unidades que representan los campos de datos iniciales que ingresan a la red, como los valores de píxeles en una imagen para una tarea de reconocimiento. Las capas ocultas son el núcleo donde se lleva a cabo el «aprendizaje profundo» de la red; en estas capas intermedias, los datos de entrada son procesados y transformados de manera compleja, permitiendo a la red aprender patrones intrincados. Finalmente, la capa de salida contiene unidades que representan el campo o los campos de destino, es decir, el resultado o la predicción de la red, como una clasificación binaria o una predicción de múltiples clases. Es importante destacar que, en el contexto del aprendizaje profundo, una red neuronal se considera «profunda» si consta de más de tres capas, incluyendo las capas de entrada y salida.
La distinción entre una «red neuronal básica» (con dos o tres capas) y un algoritmo de «aprendizaje profundo» (con más de tres capas) no es una mera convención, sino que revela una relación causal directa entre la profundidad arquitectónica de la red y su capacidad para aprender y abstraer patrones de complejidad creciente. Cuantas más capas ocultas se añaden, más la red puede construir representaciones jerárquicas de las características de los datos. Las primeras capas pueden aprender características de bajo nivel (como bordes o texturas), mientras que las capas subsiguientes combinan estas características para formar abstracciones de alto nivel (como partes de objetos o formas completas). Esta capacidad de desarrollar representaciones progresivamente más abstractas y de alto nivel es un factor crítico para el éxito de los modelos contemporáneos en la resolución de tareas altamente complejas, ya que les permite ir más allá de las simples separaciones lineales para capturar relaciones intrincadas y no lineales en los datos.
1.2. Neuronas artificiales, pesos y sesgos
Cada nodo, o neurona artificial, dentro de una red neuronal posee un peso y un umbral asociados que son fundamentales para su funcionamiento. El proceso de cálculo comienza multiplicando las entradas recibidas por la neurona por sus pesos respectivos. Estos pesos son cruciales, ya que determinan la importancia relativa de cada variable de entrada, contribuyendo de manera más o menos significativa a la suma ponderada. Posteriormente, el valor resultante de esta suma se compara con un umbral predefinido; si la salida de un nodo individual excede este umbral, el nodo se «activa», transmitiendo los datos procesados a la siguiente capa de la red. Adicionalmente, las neuronas suelen incluir un valor de «sesgo» (bias), que permite ajustar la sensibilidad de la curva de activación, proporcionando una mayor flexibilidad en la capacidad de decisión de la neurona.
La interacción entre los pesos, los sesgos y la función de activación constituye el mecanismo fundamental mediante el cual una neurona artificial adquiere la capacidad de «aprender» e identificar patrones. Los pesos modulan la influencia de cada entrada individual, determinando qué tan relevante es una pieza de información para la decisión de la neurona. Por otro lado, el sesgo actúa como un desplazamiento, permitiendo que la función de activación se mueva a lo largo del eje, lo que controla cuándo se activa una neurona. Sin el sesgo, la función de activación siempre pasaría por el origen, limitando la flexibilidad del modelo. Esta combinación de pesos y sesgos es lo que dota a la red de la capacidad de modelar relaciones complejas y no lineales en los datos, sentando las bases de su adaptabilidad y poder predictivo.
1.3. Funciones de activación: Papel y tipos comunes
Después de que las entradas ponderadas son sumadas, el resultado se canaliza a través de una función de activación, la cual es responsable de determinar la salida final del nodo. La función principal de estas funciones es introducir no linealidad en la red, una característica esencial que le permite aprender patrones complejos y no meramente relaciones lineales. Entre los ejemplos más comunes de funciones de activación se encuentran la función escalonada, la función sigmoide y la Unidad Lineal Rectificada (ReLU). La función sigmoide, por ejemplo, transforma el valor de entrada en un número comprendido entre 0 y 1, lo que la hace particularmente útil para tareas de clasificación binaria. Por otro lado, ReLU devuelve 0 si el valor de entrada es negativo y el valor original si es positivo, lo que ha demostrado ser muy eficiente en el entrenamiento de redes profundas.
La incorporación de funciones de activación no lineales representó un avance crítico que permitió a las redes neuronales trascender las limitaciones inherentes de los modelos puramente lineales, como el perceptrón simple. Sin esta capacidad de introducir no linealidad, incluso una red compuesta por múltiples capas seguiría siendo matemáticamente equivalente a una única capa lineal, lo que la haría incapaz de resolver problemas complejos como el famoso problema XOR. La elección específica de la función de activación tiene un impacto directo no solo en la capacidad de aprendizaje de la red, sino también en la mitigación de desafíos como el problema del gradiente desvanecido. Por ejemplo, el uso de ReLU en lugar de funciones como la sigmoide o tanh ayudó a acelerar el entrenamiento y a abordar el problema del gradiente desvanecido, lo que demuestra una evolución constante en la búsqueda de mayor eficiencia y robustez en el diseño de redes neuronales.
La siguiente tabla resume los componentes fundamentales de una neurona artificial:
Tabla 1: Componentes Fundamentales de una Neurona Artificial.
| Componente | Función Clave |
| Entradas (Inputs): Datos brutos que la neurona recibe. | Suministrar la información base para el procesamiento. |
| Pesos (Weights): Multiplicadores numéricos asociados a cada entrada. | Determinar la importancia relativa de cada entrada en la suma ponderada. Estos valores se ajustan durante el proceso de entrenamiento. |
| Sesgo (Bias): Un valor constante que se añade a la suma ponderada. | Ajustar la sensibilidad de la neurona, permitiendo que la función de activación se desplace y la neurona se active con diferentes umbrales, lo que aumenta la flexibilidad del modelo. |
| Suma Ponderada (Weighted Sum): El resultado de la suma de cada entrada multiplicada por su peso respectivo, más el sesgo. | Combinar las entradas de manera que reflejen su importancia relativa antes de que la neurona tome una decisión de activación. |
| Función de Activación (Activation Function): Una función matemática no lineal aplicada a la suma ponderada. | Introducir la no linealidad necesaria para que la red aprenda patrones complejos y decida si la neurona «se activa» (transmite una señal) o no. |
| Salida (Output): El valor resultante de la función de activación, que puede servir como entrada para la siguiente capa de la red o como la predicción final del modelo. | Transmitir la información procesada a la siguiente etapa de la red, o presentar el resultado final. |
2. Orígenes y pioneros de las redes neuronales
La historia de las redes neuronales es un testimonio de la perseverancia y la visión a largo plazo, con sus raíces extendiéndose mucho antes de su reciente auge de popularidad.
2.1. Primeros conceptos y contribuciones (Hebb, McCulloch & Pitts, Minsky)
Las primeras conceptualizaciones sobre la posibilidad de crear redes neuronales que funcionaran como ordenadores fueron introducidas por Warren McCulloch y Walter Pitts en 1943 , marcando un hito teórico fundamental. Estos investigadores visionarios sentaron las bases para el modelo computacional de una neurona. Posteriormente, en 1949, Donald Hebb propuso la influyente «regla de Hebb», que postula que el aprendizaje ocurre mediante cambios en la fuerza de las conexiones neuronales cuando estas son activadas simultáneamente. Sus trabajos formaron los cimientos de la Teoría de las Redes Neuronales , sugiriendo un mecanismo biológicamente plausible para el aprendizaje. Avanzando en la implementación práctica, en 1951, el matemático estadounidense Marvin Minsky desarrolló la SNARC (Stochastic Neural Analog Reinforcement Calculator), el primer simulador de redes neuronales. Este dispositivo pionero simulaba el comportamiento de una rata aprendiendo a moverse en un laberinto, ofreciendo una de las primeras demostraciones de aprendizaje en una máquina inspirada en principios neuronales.
Esta cronología del desarrollo temprano de las redes neuronales revela una progresión clara desde la conceptualización puramente teórica hasta las primeras tentativas de implementación práctica. Este patrón subraya que la visión de las redes neuronales es intrínsecamente más antigua que su reciente auge de popularidad. Las ideas fundamentales ya estaban presentes hace más de 60 años, pero su implementación práctica se vio restringida por las limitaciones de la tecnología computacional disponible en cada era. La capacidad de llevar estas ideas teóricas a modelos funcionales dependía directamente del avance en el hardware, lo que establece una relación de causa y efecto entre la disponibilidad de recursos computacionales y la viabilidad del progreso en el campo.
2.2. El Perceptrón de Frank Rosenblatt: Nacimiento y primeras limitaciones
El Dr. Frank Rosenblatt (1928 – 1971), un psicólogo estadounidense, es ampliamente reconocido como uno de los padres fundadores del Deep Learning. En 1957, Rosenblatt inventó el perceptrón en el laboratorio aeronáutico de Cornell. Este invento no solo fue una neurona artificial, sino que también dio lugar al Mark I Perceptrón, el primer ordenador diseñado específicamente para la creación de redes neuronales. Rosenblatt basó su trabajo en las ideas pioneras de McCulloch y Pitts , proponiendo una «regla de aprendizaje del perceptrón». En esencia, un perceptrón funciona como una neurona artificial que se activa (produciendo una salida binaria de 0 o 1) si la suma ponderada de sus entradas excede un umbral predeterminado, permitiendo la clasificación de datos. Para lograr esto, los datos de entrada se multiplican por coeficientes de peso, y el resultado se pasa a una función de activación que determina la salida binaria.
El perceptrón de Rosenblatt, aunque un hito crucial como la primera implementación tangible de una red neuronal con capacidad de aprendizaje, se encontró con una limitación fundamental: su incapacidad para resolver problemas no linealmente separables, como la función XOR. Esta deficiencia, sumada a las expectativas iniciales a menudo exageradas sobre las capacidades de la IA , contribuyó a lo que se conoce como el «invierno de la IA». Durante este período, la financiación y el interés en la investigación de la inteligencia artificial disminuyeron drásticamente. Este episodio histórico ilustra cómo las promesas excesivas y las limitaciones técnicas intrínsecas pueden influir significativamente en los ciclos de financiación y el ritmo de desarrollo de un campo emergente. La incapacidad del perceptrón simple para manejar problemas no lineales significó que, a pesar de su promesa inicial, no podía abordar la complejidad del mundo real, lo que llevó a una desilusión y a una reducción de la inversión en el campo.
La siguiente tabla resume los hitos clave en la historia temprana de las redes neuronales:
Tabla 2: Hitos Clave en la Historia Temprana de las Redes Neuronales:
| Pionero(s) / Evento | Contribución Clave |
| Warren McCulloch y Walter Pitts (1943) | Propusieron el primer modelo computacional de una neurona, sentando las bases teóricas para las redes neuronales artificiales. Sus ideas sobre la posibilidad de crear redes neuronales como ordenadores fueron seminales. |
| Donald Hebb (1949) | Formuló la «regla de Hebb», que describe cómo las conexiones neuronales se fortalecen con la actividad conjunta. Sus trabajos formaron las bases de la Teoría de las Redes Neuronales. |
| Marvin Minsky (1951) | Creó la SNARC (Stochastic Neural Analog Reinforcement Calculator), el primer simulador de redes neuronales, que simulaba el comportamiento de una rata aprendiendo en un laberinto. |
| Frank Rosenblatt (1957) | Inventó el Perceptrón, la primera red neuronal artificial con capacidad de aprendizaje, y el Mark I Perceptrón, el primer hardware dedicado específicamente para redes neuronales. Propuso la «regla de aprendizaje del perceptrón». |
| Primer «Invierno de la IA» (mediados de los 60s) | Periodo de desilusión y reducción de financiación en la investigación de IA debido a las limitaciones del perceptrón simple (incapacidad de resolver problemas no lineales como XOR) y promesas de traducción automática no materializadas. |
3. La evolución desde el perceptrón multicapa (MLP)
El «invierno de la IA» fue un período de estancamiento, pero también de reflexión, que impulsó la búsqueda de arquitecturas más robustas y capaces de superar las limitaciones fundamentales de los modelos iniciales. La respuesta llegó con el desarrollo del Perceptrón Multicapa.
3.1. Superando las limitaciones del Perceptrón simple
Mientras que un perceptrón de capa única está intrínsecamente limitado a aprender y clasificar únicamente funciones que son linealmente separables , el Perceptrón Multicapa (MLP) representa un avance significativo al superar esta restricción fundamental. Esta arquitectura mejorada ofrece una potencia de cálculo sustancialmente superior, permitiéndole aproximar cualquier función compleja , lo que lo convierte en una herramienta mucho más versátil para el aprendizaje automático. La evolución del perceptrón simple al MLP no fue meramente un incremento en la complejidad arquitectónica, sino una solución fundamental al desafío de la no-linealidad en el aprendizaje automático. El perceptrón simple no podía resolver problemas como la función XOR, que no es linealmente separable. Al añadir capas ocultas y funciones de activación no lineales, el MLP pudo modelar límites de decisión complejos y no lineales. Este avance marcó el verdadero punto de inflexión para el potencial de las redes neuronales, permitiéndoles modelar relaciones intrincadas en datos del mundo real y trascender las limitaciones teóricas que habían obstaculizado el progreso del campo hasta entonces.
3.2. Arquitectura del MLP y el aprendizaje de patrones «no lineales»
Un Perceptrón Multicapa (MLP) se caracteriza por su organización en tres tipos de capas: una capa de entrada, una o más capas ocultas, y una capa de salida. Cada nodo dentro de las capas ocultas procesa la información recibida de la capa anterior, multiplicando los valores por pesos específicos y luego pasando el resultado a través de una función de activación no lineal, como ReLU (Rectified Linear Unit) o Sigmoid. Estas funciones de activación son esenciales, ya que son las que permiten a los MLPs aprender y representar relaciones no lineales en los datos, una capacidad que los modelos lineales no poseen. La profundidad de estas capas ocultas es un factor crítico, ya que habilita al modelo para abstraer características útiles y construir conceptos de alto nivel a partir de los datos de entrada, mejorando su capacidad de generalización.
La capacidad del MLP para aprender relaciones no lineales, lograda mediante la combinación de múltiples capas ocultas y la aplicación de funciones de activación no lineales, lo consolida como un «aproximador de funciones» universal. Esto significa que, en teoría, un MLP con una sola capa oculta y un número suficiente de neuronas puede aproximar cualquier función continua. Este diseño implica que el MLP puede descomponer una función compleja en una serie de regiones lineales o casi lineales interconectadas. Cada neurona en una capa oculta puede aprender a identificar una característica o un patrón específico, y la combinación de estas neuronas en capas subsiguientes permite la creación de abstracciones más complejas. Este enfoque permite una representación más eficiente y una mejor generalización a conjuntos de datos complejos, lo que representa un salto cualitativo respecto a los modelos más simples que carecían de la capacidad de capturar tales complejidades.
3.3. El Algoritmo de retropropagación (Backpropagation)
El entrenamiento de los Perceptrones Multicapa (MLPs) se lleva a cabo mediante el algoritmo de retropropagación (backpropagation), un proceso iterativo que calcula los gradientes de una función de pérdida con respecto a los parámetros del modelo y los actualiza progresivamente para minimizar dicha pérdida. Este algoritmo es fundamental para el aprendizaje de la red, ya que implica propagar el error desde la capa de salida hacia atrás, a través de las capas ocultas hasta la capa de entrada, ajustando los pesos de las conexiones en cada paso.
La retropropagación fue el algoritmo pivotal que hizo posible el entrenamiento eficiente de MLPs profundos, al permitir el ajuste sistemático de millones de pesos. Antes de su desarrollo, el entrenamiento de redes con múltiples capas ocultas era computacionalmente inviable. El algoritmo calcula cómo cada peso contribuye al error total de la red y luego ajusta esos pesos en la dirección que reduce el error. Sin un método eficaz para ajustar los parámetros de la red de esta manera, el vasto potencial de las capas ocultas para aprender representaciones complejas no podría haberse explotado en la práctica. Por lo tanto, la retropropagación no es solo un algoritmo de optimización, sino el motor que impulsa la capacidad de aprendizaje del MLP, transformando una arquitectura teóricamente poderosa en una herramienta práctica y efectiva.
4. La Era de las redes neuronales convolucionales (CNNs)
Con el avance de la computación y la necesidad de procesar datos con estructuras espaciales intrínsecas, como las imágenes, surgió una nueva clase de redes neuronales: las Redes Neuronales Convolucionales.
4.1. Introducción a las CNNs: Diseño para datos visuales
Una Red Neuronal Convolucional (CNN) es un tipo especializado de red neuronal artificial, diseñada fundamentalmente para el análisis de datos visuales. Estas redes se distinguen por su rendimiento superior al procesar entradas de señal de imagen, voz o audio, en comparación con otras arquitecturas neuronales. Las CNNs operan procesando las imágenes de entrada a través de múltiples capas, donde las capas iniciales se encargan de identificar características sencillas como bordes y líneas. A medida que los datos avanzan a través de las capas más profundas de la CNN, la red progresivamente reconoce patrones, formas y, finalmente, objetos complejos completos. Este enfoque jerárquico de extracción de características es lo que ha consolidado a las CNNs como el estándar de facto en el campo de la visión por computadora y el procesamiento de imágenes.
La especialización de las CNNs en el procesamiento de datos visuales (y datos con estructura de cuadrícula, como espectrogramas de audio) representa un cambio estratégico significativo en el desarrollo de redes neuronales. Se pasó de arquitecturas de propósito general, como los MLPs, a modelos optimizados para dominios específicos. Esta tendencia en la investigación de IA demuestra la importancia de diseñar arquitecturas que exploten la estructura inherente de ciertos tipos de datos. Al incorporar suposiciones sobre la naturaleza de las imágenes (por ejemplo, la localidad espacial y la invarianza traslacional), las CNNs pueden lograr una eficiencia y una precisión considerablemente superiores que los MLPs generales para estas tareas. Esto ha llevado a avances sin precedentes en la visión por computadora, permitiendo aplicaciones como el reconocimiento facial, la detección de objetos y los vehículos autónomos.
4.2. Componentes clave: Capas convolucionales, de agrupamiento (Pooling) y totalmente conectadas
Las arquitecturas de CNNs se construyen principalmente a partir de tres tipos de capas interconectadas, cada una con un propósito específico en el proceso de extracción y clasificación de características: la capa convolucional, la capa de agrupamiento (pooling) y la capa totalmente conectada (FC).
La capa convolucional es el componente fundamental y, a menudo, la primera capa en una red convolucional. Consiste en un conjunto de filtros o kernels que se deslizan sobre la imagen de entrada, realizando operaciones de producto punto para generar «mapas de características» o «mapas de activación». Cada neurona en una capa convolucional está conectada únicamente a una pequeña región de la capa anterior, conocida como campo receptivo. Una característica distintiva y crucial es que estos filtros comparten los mismos parámetros (pesos y sesgos) a través de todo el campo visual. Esta propiedad, conocida como pesos compartidos, confiere a la red una valiosa propiedad de equivariancia traslacional, es decir, la capacidad de detectar una característica (como un borde o una textura) sin importar su ubicación específica en la imagen. Esto reduce drásticamente el número de parámetros a aprender, haciendo el modelo más eficiente y menos propenso al sobreajuste.
La capa de agrupamiento (pooling), ubicada generalmente después de una capa convolucional, tiene como objetivo principal reducir las dimensiones espaciales de los mapas de características resultantes. Las operaciones comunes incluyen el agrupamiento máximo (max pooling) o el agrupamiento promedio (average pooling), donde se toma el valor máximo o promedio de subregiones rectangulares. Esta reducción de dimensionalidad no solo disminuye la complejidad computacional y la cantidad de parámetros, sino que también ayuda a construir una invarianza traslacional local. Esto significa que la red se vuelve más robusta a pequeñas variaciones o desplazamientos en la posición de las características de entrada, ya que la información esencial se conserva incluso si la característica se mueve ligeramente.
Finalmente, la capa totalmente conectada (FC) constituye la capa final o las capas finales de una CNN. En esta etapa, las características de alto nivel extraídas por las capas convolucionales y de agrupamiento son «aplanadas» (convertidas en un vector unidimensional) y alimentadas a estas capas densas. Aquí, cada neurona está conectada a todas las neuronas de la capa anterior, similar a un MLP tradicional. Estas capas son responsables de la clasificación final o la predicción basada en las características aprendidas a lo largo de las capas anteriores.
La sinergia entre las capas convolucionales, las capas de agrupamiento y las capas totalmente conectadas es la piedra angular del éxito de las CNNs. Las capas convolucionales realizan una extracción jerárquica y eficiente de características mediante pesos compartidos, identificando patrones locales. Las capas de agrupamiento reducen la dimensionalidad y otorgan invarianza a pequeñas traslaciones, haciendo el modelo más robusto. Las capas totalmente conectadas, por su parte, realizan la clasificación final utilizando las representaciones de alto nivel aprendidas. Esta arquitectura modular y jerárquica no solo optimiza el procesamiento de datos visuales de manera computacionalmente eficiente, sino que también emula de manera abstracta cómo el sistema visual biológico procesa la información, permitiendo a las CNNs aprender representaciones progresivamente más abstractas y complejas de las imágenes.
5. Arquitecturas emblemáticas de CNNs
El éxito de las CNNs se materializó a través de diversas arquitecturas que marcaron hitos significativos en la visión por computadora, cada una aportando innovaciones clave.
5.1. LeNet-5: El Precursor de la visión por computadora
LeNet-5, introducida por Yann LeCun y su equipo en 1998, es reconocida como una de las primeras arquitecturas de redes neuronales convolucionales que demostró el potencial del aprendizaje profundo en aplicaciones prácticas. Fue diseñada específicamente para el reconocimiento de caracteres manuscritos y mecanografiados, una función que la hizo popular en servicios postales y bancarios.
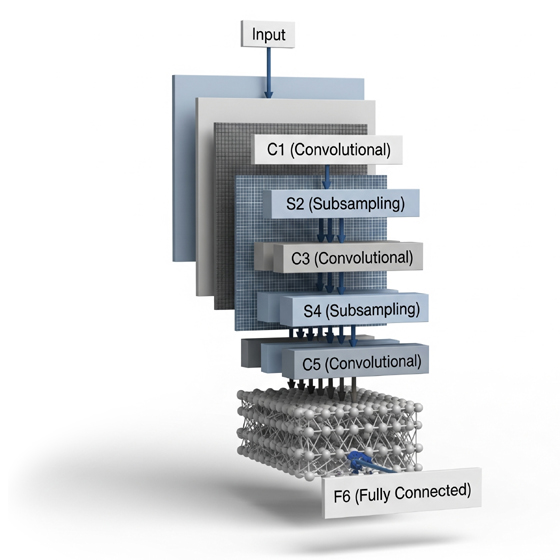
La arquitectura de LeNet-5 es notable por su simplicidad y eficacia, consistiendo en siete capas con parámetros aprendibles. Recibe una imagen en escala de grises de 32×32 píxeles como entrada. La red se compone de tres conjuntos de capas convolucionales combinadas con capas de agrupamiento (subsampling), seguidas por dos capas totalmente conectadas y, finalmente, una capa de salida con una función Softmax para la clasificación. Las capas convolucionales (C1 y C3) utilizan filtros para extraer características espaciales, mientras que las capas de subsampling (S2 y S4) reducen las dimensiones espaciales de los mapas de características, contribuyendo a la invarianza traslacional. La función de activación utilizada en estas capas es la tangente hiperbólica (tanh).
Las contribuciones de LeNet-5 fueron fundamentales. Introdujo conceptos que se convertirían en la base de las CNNs modernas, como las capas convolucionales y de subsampling (pooling), demostrando su capacidad para aprender representaciones jerárquicas de características. Su éxito en el reconocimiento de dígitos manuscritos pavimentó el camino para una nueva era en la visión por computadora, influenciando el diseño y desarrollo de arquitecturas posteriores como AlexNet, VGGNet y ResNet.
5.2. AlexNet: El Despegue del Deep Learning en visión
AlexNet, desarrollada en 2012 por Alex Krizhevsky, Ilya Sutskever y Geoffrey Hinton en la Universidad de Toronto, marcó un punto de inflexión en la historia del deep learning. Su desempeño dominante en el ImageNet Large Scale Visual Recognition Challenge (ILSVRC) de 2012, donde logró una tasa de error top-5 del 15.3% (más de 10.8 puntos porcentuales mejor que el segundo clasificado), demostró el potencial sin precedentes de las redes convolucionales profundas a gran escala. Este triunfo no solo significó una victoria en una competición, sino que también inauguró la era actual del deep learning.
La arquitectura de AlexNet consta de ocho capas: cinco capas convolucionales para la extracción de características, seguidas de tres capas totalmente conectadas para la clasificación. La red fue diseñada para procesar imágenes RGB de 227x227x3 píxeles. Sus innovaciones clave fueron cruciales para su éxito:
- Aceleración por GPU: AlexNet fue pionera en el uso intensivo de unidades de procesamiento gráfico (GPUs) para el entrenamiento. Se entrenó durante cinco o seis días utilizando dos GPUs Nvidia GTX 580, lo que demostró que el poder de procesamiento paralelo era indispensable para manejar conjuntos de datos masivos como ImageNet. Las CPUs de la época eran insuficientes para esta tarea.
- Función de Activación ReLU: A diferencia de las funciones tradicionales como sigmoide o tanh, AlexNet empleó Rectified Linear Units (ReLU). ReLU introdujo no linealidad de manera más eficiente y aceleró significativamente el entrenamiento al mitigar el problema del gradiente desvanecido, haciendo posible entrenar redes mucho más profundas.
- Regularización Dropout: Para reducir el sobreajuste, se utilizó la técnica de dropout, que desactiva aleatoriamente un porcentaje de neuronas durante el entrenamiento, obligando a la red a aprender representaciones más robustas.
- Aumento de Datos (Data Augmentation): Se aplicaron técnicas de aumento de datos sobre la marcha (como recortes aleatorios y volteos horizontales) para expandir artificialmente el tamaño del conjunto de entrenamiento y mejorar la resiliencia y generalización del modelo.
El impacto de AlexNet fue transformador. Catalizó la creación de arquitecturas más profundas y complejas, como VGGNet y ResNet. Sus avances trascendieron la identificación de imágenes, extendiéndose a campos como el procesamiento del lenguaje natural, los vehículos autónomos y la imagen médica. Además, AlexNet impulsó una revolución en la aceleración de hardware, demostrando la eficacia de las GPUs en el entrenamiento de redes profundas y sentando las bases para el desarrollo de unidades de procesamiento de tensores (TPUs) y otros aceleradores de IA.
5.3. VGGNet: La importancia de la profundidad y la uniformidad
VGGNet, introducida en 2014 por el Grupo de Geometría Visual (VGG) de la Universidad de Oxford, amplió las ideas de AlexNet al explorar la importancia de la profundidad de la red en el rendimiento de la clasificación de imágenes. Su principal contribución fue demostrar que aumentar la profundidad de la red, mediante la apilación de múltiples capas convolucionales pequeñas (filtros de 3×3), podía mejorar significativamente el rendimiento en tareas de reconocimiento de imágenes a gran escala.
Los principios de diseño arquitectónico de VGG-19 (una variante común) se centraron en la uniformidad y la profundidad. Utilizó consistentemente filtros convolucionales de 3×3 píxeles y funciones de activación ReLU a lo largo de toda la red. Esta simplicidad en el diseño, combinada con una mayor profundidad, permitió a la red aprender características más complejas.
El impacto y el legado de VGGNet son considerables. Su arquitectura, aunque computacionalmente costosa, sirvió como línea base en numerosas investigaciones académicas y demostró de manera contundente que la profundidad era un factor clave para el rendimiento superior en tareas de reconocimiento de imágenes. Modelos posteriores como ResNet e Inception se inspiraron en los principios de profundidad y uniformidad establecidos por VGG, y sus pesos pre-entrenados en ImageNet se utilizan ampliamente en el aprendizaje por transferencia para diversas tareas de visión por computadora, incluyendo la detección de objetos y la segmentación de imágenes.
5.4. ResNet: Conexiones residuales para redes ultradeep
Residual Networks (ResNet), propuesta en 2015 por investigadores de Microsoft Research, representó una innovación crucial que permitió el entrenamiento de redes neuronales extremadamente profundas, llegando a ganar el ImageNet classification challenge de 2015. El problema principal que ResNet abordó fue la «degradación» en redes muy profundas, donde, paradójicamente, al aumentar el número de capas, el rendimiento del entrenamiento y la prueba comenzaba a deteriorarse. Esto se debía, en parte, a los problemas de gradientes desvanecidos o explosivos, que dificultaban el ajuste de los pesos en las capas iniciales durante la retropropagación.
La innovación fundamental de ResNet reside en la introducción de bloques residuales y conexiones de salto (skip connections o shortcut connections). En lugar de que cada capa aprenda una nueva función de mapeo H(x), ResNet propone que las capas aprendan una «función residual» F(x) = H(x) - x. La salida de un bloque residual se convierte entonces en H(x) = F(x) + x, donde x es la entrada del bloque. Las conexiones de salto implementan esto realizando un mapeo de identidad que conecta directamente la entrada de un bloque con su salida, saltándose una o más capas intermedias.
Este enfoque ofrece varias ventajas:
- Mitigación del Gradiente Desvanecido: Las conexiones de salto proporcionan una ruta alternativa para que los gradientes fluyan hacia atrás a través de la red, lo que ayuda a mitigar el problema del gradiente desvanecido y permite entrenar redes con cientos de capas sin que el aprendizaje se detenga.
- Facilita el Aprendizaje: Aprender una función residual
F(x)(que representa un pequeño ajuste o «residuo» a la entrada) es a menudo más fácil para la red que aprender una transformación completamente nuevaH(x). Si una capa no es útil, la red puede simplemente aprender a hacer queF(x)sea cero, permitiendo que la identidadxpase a través de la conexión de salto sin cambios, lo que facilita la optimización.
El impacto de ResNet fue inmenso. Habilitó el entrenamiento de redes neuronales extremadamente profundas con un rendimiento superior y se convirtió en un motivo arquitectónico común en el deep learning, siendo adoptado incluso por arquitecturas posteriores como los modelos Transformer.
6. Redes neuronales recurrentes (RNNs) y LSTM
Mientras que las CNNs revolucionaron el procesamiento de datos espaciales, la necesidad de manejar secuencias de datos, donde el orden y el contexto temporal son cruciales, llevó al desarrollo de las Redes Neuronales Recurrentes.
6.1. Introducción a las RNNs: Procesamiento de datos secuenciales
Las Redes Neuronales Recurrentes (RNNs) son un tipo específico de red neuronal artificial diseñada para reconocer características secuenciales dentro de un conjunto de datos y utilizar estos patrones para predecir el siguiente escenario probable en la secuencia. A diferencia de las redes neuronales prealimentadas (como los MLPs o CNNs), que procesan cada entrada de forma independiente, las RNNs utilizan bucles de retroalimentación que les permiten pasar información de un paso de tiempo al siguiente. Esto significa que la salida de un paso de tiempo anterior se retroalimenta como entrada para el paso de tiempo actual, dotando a la red de una especie de «memoria a corto plazo» que le permite recordar y utilizar entradas previas para futuras predicciones.
Este mecanismo las hace particularmente adecuadas para aplicaciones que involucran datos secuenciales, donde el contexto de los elementos anteriores es vital para comprender los elementos actuales o futuros. Las aplicaciones más comunes de las RNNs incluyen el Procesamiento del Lenguaje Natural (PLN), como la traducción automática, la clasificación de sentimientos y la generación de texto. También son ampliamente utilizadas en el reconocimiento de voz, donde deben identificar y predecir palabras y frases en una secuencia de audio. Otros dominios incluyen la predicción de series temporales, como la predicción del mercado de valores o la previsión de ventas.
A pesar de sus capacidades, las RNNs tradicionales presentan limitaciones significativas. El problema más notorio es el problema del gradiente desvanecido o explosivo. Durante el entrenamiento, cuando los gradientes se propagan hacia atrás a través de muchas capas (o pasos de tiempo en una secuencia larga), pueden volverse exponencialmente pequeños (desvanecidos) o exponencialmente grandes (explosivos). Un gradiente desvanecido impide que la red aprenda dependencias a largo plazo, ya que los ajustes de peso en las capas iniciales se vuelven insignificantes. Un gradiente explosivo puede desestabilizar el entrenamiento. Esto significa que las RNNs básicas tienen dificultades para retener información relevante de pasos de tiempo muy lejanos en una secuencia, limitando su capacidad para manejar dependencias a largo plazo.
6.2. LSTM: La Solución a las dependencias a largo plazo
Para superar las limitaciones del gradiente desvanecido en las RNNs tradicionales, se desarrolló un tipo especializado de red neuronal recurrente: las redes de Memoria a Corto y Largo Plazo (LSTM). Las LSTMs están diseñadas específicamente para aprender, procesar y clasificar datos secuenciales, destacando por su capacidad para aprender dependencias a largo plazo entre unidades de tiempo de datos.
La arquitectura de una unidad LSTM es más sofisticada que la de una neurona recurrente simple, incorporando un mecanismo de memoria más complejo. Además del estado oculto (h), una unidad LSTM mantiene un «estado de celda» (C) que actúa como una memoria de largo plazo. El flujo de información dentro y fuera de esta celda de memoria es regulado por un conjunto de «compuertas» (gates), que son pequeñas redes neuronales sigmoidales que controlan selectivamente qué información se permite pasar.
Las tres compuertas principales en una unidad LSTM son:
- Compuerta de Olvido (Forget Gate): Decide qué información del estado de celda anterior debe ser descartada o retenida. Multiplica el valor de la celda de memoria por un número entre 0 (borrar) y 1 (mantener todo).
- Compuerta de Entrada (Input Gate o Write Gate): Determina qué nueva información del paso de tiempo actual es relevante y debe ser añadida al estado de celda. Controla el flujo de nueva información hacia la memoria.
- Compuerta de Salida (Output Gate): Regula qué parte del estado de celda actual se expone como el estado oculto de la unidad (la salida) para el siguiente paso de tiempo o para la capa siguiente. Multiplica el estado de celda por un número entre 0 (sin salida) y 1 (preservar salida).
Al controlar el flujo de información de esta manera, las LSTMs logran un «carrusel de errores» continuo, donde los errores se preservan y se retroalimentan a las compuertas hasta que estas aprenden a cortar el valor. Esto elimina eficazmente el problema del gradiente desvanecido, permitiendo que la red aprenda de secuencias que se extienden a lo largo de cientos de pasos de tiempo.
Las aplicaciones de las LSTMs son vastas y abarcan múltiples dominios:
- Procesamiento del Lenguaje Natural (PLN): Son muy útiles en traducción automática, análisis de sentimientos, generación de texto coherente, y asistentes virtuales, donde la comprensión del contexto a largo plazo es crucial.
- Predicción y Series Temporales: Se aplican en la predicción del clima, el mantenimiento predictivo en la industria y el análisis de señales biomédicas, debido a su capacidad para modelar dependencias temporales.
- Visión por Computadora: Utilizadas en el reconocimiento de actividad en videos y la segmentación de imágenes, ya que los videos son secuencias de imágenes.
- Otros: Biomedicina y salud (diagnóstico médico, predicción de condiciones futuras), robótica (control temporal, planificación de acciones), y generación de música.
7. La revolución del Transformer
A pesar de los avances de las LSTMs en el manejo de dependencias a largo plazo, su naturaleza secuencial inherente limitaba la paralelización del entrenamiento. Esta limitación fue abordada por una arquitectura revolucionaria: el Transformer.
7.1. Introducción al modelo Transformer: «Attention Is All You Need»
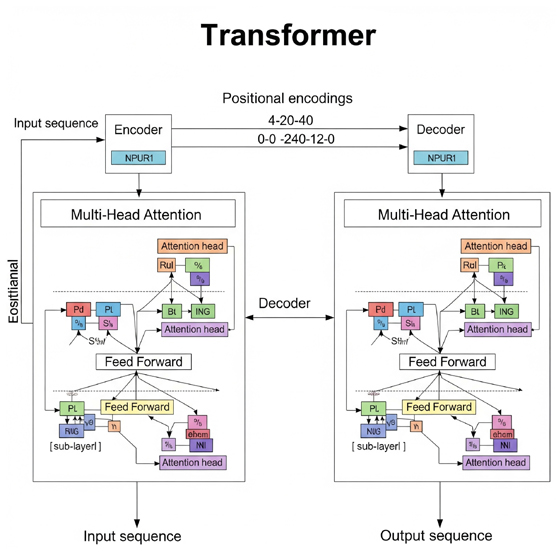
El modelo Transformer es un tipo de arquitectura de red neuronal que sobresale en el procesamiento de datos secuenciales y está prominentemente asociado con los modelos de lenguaje grandes (LLMs). Fue introducido en un artículo seminal de 2017 titulado «Attention Is All You Need» por un equipo de investigadores de Google. Este trabajo revolucionó el campo al proponer una arquitectura de red que prescindía por completo de las unidades recurrentes (RNNs) y las convoluciones (CNNs), confiando exclusivamente en un mecanismo de autoatención.
La principal ventaja de los Transformers sobre sus predecesores, como las RNNs y LSTMs, radica en su capacidad para procesar secuencias de datos de manera paralela, en lugar de secuencialmente. Las RNNs procesan los elementos de una secuencia uno a la vez y en un orden específico, lo que inherentemente serializa el proceso y lo hace lento para secuencias largas. El Transformer, al eliminar la recurrencia, permite que todas las partes de la secuencia de entrada se procesen simultáneamente, lo que reduce drásticamente el tiempo de entrenamiento y mejora la eficiencia. Esta característica es fundamental para el escalado a los enormes conjuntos de datos utilizados en el entrenamiento de los LLMs modernos.
7.2. El Mecanismo de autoatención (Self-Attention)
La característica central de los modelos Transformer es su mecanismo de autoatención, también conocido como intra-atención. Este mecanismo permite a la red detectar las relaciones o dependencias entre cada parte de una secuencia de entrada. En esencia, la autoatención permite que el modelo «pese» la importancia de los diferentes tokens o palabras en una secuencia de entrada para comprender mejor las relaciones contextuales entre ellos, independientemente de su posición.
El funcionamiento se basa en la generación de tres vectores para cada token de entrada: un vector de consulta (Query, Q), un vector de clave (Key, K) y un vector de valor (Value, V). El vector de consulta representa la información que un token específico está «buscando», mientras que los vectores de clave representan la información que cada token contiene. Los «puntajes de alineación» se calculan como el producto punto entre el vector de consulta de un token y los vectores de clave de todos los demás tokens en la secuencia. Estos puntajes se escalan (para evitar gradientes pequeños con valores grandes de
d_k) y se pasan a una función Softmax para convertirlos en «pesos de atención», que luego se aplican a los vectores de valor. El resultado es una suma ponderada de los valores, donde los pesos reflejan la relevancia de cada token para el token actual.
Para mejorar aún más esta capacidad, los Transformers emplean el mecanismo de atención multi-cabeza (Multi-Head Attention). Este enfoque permite que el modelo realice el cálculo de atención múltiples veces en paralelo, utilizando diferentes proyecciones lineales de los vectores Q, K y V para cada «cabeza» de atención. Cada cabeza aprende a enfocarse en diferentes aspectos de las relaciones dentro de la secuencia, lo que permite al modelo capturar una gama más diversa y rica de dependencias simultáneamente. Las salidas de todas las cabezas se concatenan y se transforman linealmente para producir la salida final.
La capacidad de paralelización es un beneficio clave de la autoatención. Al calcular los pesos de atención a través de todas las partes de la secuencia de entrada simultáneamente, el entrenamiento de los modelos de lenguaje grandes puede dividirse en lotes y procesarse concurrentemente en múltiples GPUs. Esto reduce drásticamente el tiempo de entrenamiento y los costos computacionales en comparación con los modelos secuenciales.
7.3. Impacto y aplicaciones del Transformer
El impacto de los modelos Transformer en el campo de la inteligencia artificial ha sido verdaderamente revolucionario, extendiéndose mucho más allá de su aplicación inicial en la traducción automática.
- Procesamiento del Lenguaje Natural (PLN): Los Transformers han transformado radicalmente el PLN, convirtiéndose en la arquitectura fundamental para la mayoría de los modelos de lenguaje grandes (LLMs) modernos, como BERT de Google y la serie GPT de OpenAI (incluido ChatGPT). Su capacidad para aprender el contexto y el significado de las palabras rastreando las relaciones en datos secuenciales, incluso a largas distancias, los hace increíblemente efectivos para tareas como la traducción automática, el análisis de sentimientos, la generación de texto coherente y realista, el resumen de documentos, la respuesta a preguntas y la identificación de entidades nombradas. Por ejemplo, pueden desambiguar palabras como «banco» (institución financiera o orilla de río) al considerar el contexto completo de la oración.
- Visión por Computadora: Aunque las CNNs dominaron tradicionalmente la visión por computadora, los Transformers han comenzado a irrumpir en este campo con arquitecturas como los Vision Transformers (ViTs). Los ViTs dividen una imagen en parches, los convierten en incrustaciones (embeddings) y aplican mecanismos de autoatención para capturar características relevantes, logrando un rendimiento impresionante en tareas como la clasificación y detección de objetos.
- Otros Dominios: La influencia de los Transformers se ha extendido a una amplia gama de aplicaciones, incluyendo el reconocimiento de voz (donde modelos como Speech-Transformer y Conformer combinan CNNs con autoatención) , el aprendizaje por refuerzo, el procesamiento de audio, el aprendizaje multimodal, la robótica e incluso el juego de ajedrez.
- Pre-entrenamiento y Ajuste Fino: Un paradigma común para el uso de Transformers implica el pre-entrenamiento en grandes conjuntos de datos genéricos no etiquetados (como vastos corpus de texto), seguido de un ajuste fino (fine-tuning) supervisado en conjuntos de datos más pequeños y específicos para una tarea particular. Esta estrategia permite que los modelos aprendan representaciones generales y luego se adapten eficientemente a tareas específicas con menos datos.
En resumen, los modelos Transformer han transformado la inteligencia artificial al permitir que los modelos comprendan patrones complejos, capturen dependencias a largo alcance de manera eficiente y aceleren el proceso de entrenamiento. Esto ha llevado a la creación de tecnologías de vanguardia en numerosas industrias, redefiniendo lo que es posible en la interacción entre humanos y máquinas.
8. Conclusiones
El recorrido por la historia y la evolución de las redes neuronales revela una trayectoria de constante innovación, impulsada por la ambición de emular la inteligencia humana y la necesidad de superar limitaciones técnicas. Desde los primeros conceptos teóricos de McCulloch y Pitts en 1943 y la regla de Hebb en 1949, hasta los primeros simuladores como la SNARC de Minsky en 1951, los cimientos de este campo se construyeron sobre la inspiración biológica.
El Perceptrón de Frank Rosenblatt en 1957 fue un hito crucial, al ser la primera neurona artificial con capacidad de aprendizaje y el primer hardware dedicado. Sin embargo, su incapacidad para resolver problemas no lineales, como el XOR, llevó a un período de desilusión conocido como el «invierno de la IA». Este estancamiento fue superado por el Perceptrón Multicapa (MLP), cuya arquitectura con múltiples capas ocultas y funciones de activación no lineales le permitió aprender patrones complejos y no lineales, actuando como un aproximador universal de funciones. El algoritmo de retropropagación fue la clave para entrenar eficientemente estos MLPs, permitiendo el ajuste sistemático de millones de parámetros.
La era de las Redes Neuronales Convolucionales (CNNs) marcó una especialización crucial para el procesamiento de datos visuales. Arquitecturas como LeNet-5 sentaron las bases, mientras que AlexNet demostró el poder de las CNNs a gran escala, impulsando el uso de GPUs y la adopción de funciones ReLU. VGGNet enfatizó la importancia de la profundidad y la uniformidad, y ResNet resolvió el problema de la degradación en redes ultraprofundas mediante sus innovadoras conexiones residuales, permitiendo el entrenamiento de modelos con cientos de capas.
Las Redes Neuronales Recurrentes (RNNs) surgieron para manejar datos secuenciales, introduciendo la noción de memoria a corto plazo a través de bucles de retroalimentación. No obstante, su limitación con las dependencias a largo plazo y el problema del gradiente desvanecido llevaron al desarrollo de las LSTMs. Las LSTMs, con sus sofisticadas compuertas de olvido, entrada y salida, revolucionaron el procesamiento de secuencias al permitir que la información relevante persistiera a lo largo de extensos pasos de tiempo, haciendo posibles avances significativos en el procesamiento del lenguaje natural y las series temporales.
Finalmente, el modelo Transformer, introducido en 2017, representó una disrupción al abandonar la recurrencia y las convoluciones en favor de un mecanismo de autoatención. Esta arquitectura no solo mejoró la capacidad de los modelos para capturar dependencias a largo alcance y comprender el contexto de manera más profunda, sino que también habilitó la paralelización masiva del entrenamiento, acelerando drásticamente el desarrollo de modelos de lenguaje grandes (LLMs). La autoatención multi-cabeza permite al modelo enfocarse en múltiples aspectos de las relaciones dentro de una secuencia simultáneamente, lo que ha llevado a un rendimiento sin precedentes en PLN, visión por computadora y otros dominios.
En retrospectiva, la evolución de las redes neuronales es una narrativa de superación de límites: de la linealidad a la no linealidad, de la memoria a corto plazo a las dependencias a largo plazo, y de los procesos secuenciales a la paralelización masiva. Cada avance ha habilitado nuevas capacidades y aplicaciones, transformando fundamentalmente la inteligencia artificial y su impacto en la sociedad. El camino desde el Perceptrón hasta el Transformer no es solo una historia de algoritmos, sino de cómo la ingeniería y la ciencia computacional han permitido que una idea inspirada en la biología se convierta en una de las fuerzas tecnológicas más potentes de nuestro tiempo.
—————————————————-
Fuentes: